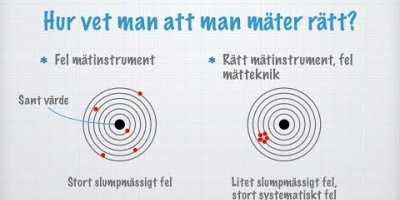
Reduktion
Fråga eleverna, vad är en expert?
- En som kan nästan allt om nästan ingenting!
Hur ska man angripa ett problem?
Röntgad högklackad stövel (med fot). Exempel: Bilen startar inte på morgonen. Vad gör du?
- Du börjar inte med att plocka isär hela bilen, och sätta ihop den igen, eller hur?
- Du börjar inte med att ta en kurs i bilmekande, eller hur?
- Du börjar med att undersöka en liten grej i taget!
Exempel Schizofreni - hur hitta ett botemedel?
- Du börjar inte med att ge patienten alla möjliga kemikalier, eller hur?
- Hur ska man angripa problemet?
- Sjukdomens orsaker
- Hjärnans fysiologi
- Hjärnans kemi
- Miljöns betydelse
- "You name it!"
För att kunna angripa ett problem, måste du reducera det.
- Liten, greppbar fråga, som har ett entydigt svar
- Ett eller ett fåtal experiment kan ge svar på frågan
- Samla fakta
- Dra slutsatser
Kan schizofreni bero på användandet av högklackade skor?
Signifikanta mätningar
Kvanitativa mätningar påverkas alltid av slumpen.
Typexempel 1: Bestämning av syrahalten i vinäger/saltsyra?
- Fick alla exakt samma resultat? Varför inte? Slumpen!
Normalfördelningskurva. Typexempel 2: Jag ska be er mäta hur lång jag är, så exakt som möjligt
- Kommer alla att få samma resultat? Varför inte? Slumpen!
Fråga: Är män längre än kvinnor?
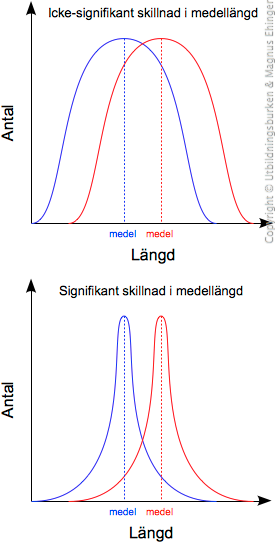
Medellängden är densamma i båda mätningarna, men i det nedre fallet är skillnaden mellan de blåa och de röda signifikant.Intuitivt vet vi, att ja, det är de.
Ställ upp klassens män och kvinnor i en "line-up".
Vi kan se att männen är längre än kvinnorna. Men beror detta på slumpen, eller är det verkligen så?
Normalfördelning
När vi mäter, kommer mätningarna att fördela sig längs en normalfördelning.
Män är i genomsnitt 179,4 cm långa, kvinnor är 165,5 cm (källa).
- Längden av kvinnor och män kommer att fördela sig på två olika normalfördelningskurvor.
Om de två normalfördelningskurvorna är nära varandra, är det stor sannolikhet att skillnaden beror på slumpen.
Om de två normalfördelningskurvorna är långt ifrån varandra, är det stor sannolikhet att skillnaden inte beror på slumpen.
Man säger att det finns en signifikant skillnad mellan de två grupperna av mätvärden.
- Om det är är mer än 95% chans att skillnaden inte beror på slumpen, kallas det för enstjärnig signifikans (*).
- 99% – (**)
- 99,9% – (***)
Exempel: Vi testar läkemedel
"Pillertrillare".
- En grupp patienter får aktiv substans
- En grupp patienter får placebo
- Varken patienter eller försöksledare vet vem som får vad - försöket är dubbelblint.
- Fråga 1: Blir patienter som får aktiv substans friskare än patienter som får placebo?
- Fråga 2: Är skillnaden signifikant?
- Endast om skillnaden är signifikant, kan man med någorlunda säkerhet säga att läkemedlet har någon verkan.
- Annars kanske tillfrisknandet beror på placeboeffekten.
Kausalitet och korrelation
Okej, där finns ett samband, t.ex. mellan att äta medicin och att bli frisk. Men vad beror den på?
- Ex. förkylning: Man låter bli att medicinera och blir frisk på 14 dagar, eller man medicinerar och blir frisk på två veckor...
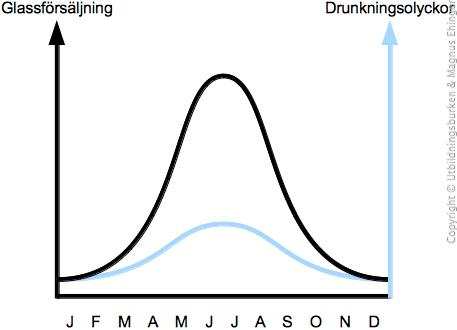Sambandet mellan glassförsäljning och drunkningsolyckor. Kausalitet: Orsakssamband
- Det finns en direkt orsak till sambandet
Korrelation
- Sambandet mellan de båda faktorerna beror på en tredje, yttre omständighet.
Exempel: Glassförsäljning och drunkningsolyckor.
Tydligt samband!
Även om två händelser korrelerar, behöver inte den ena händelsen vara orsaken till den andra.Men var har vi kausalsambandet och korrelationen, egentligen?
En annan klassiker: Asfaltens konsistens och frekvensen hjärtattacker
Ju mjukare asfalt, desto fler hjärtattacker.
- Det finns en korrelation mellan asfaltens konsistens och antalet hjärtattacker.
- Kan du hitta kausalsambandet?
En tredje klassiker: Solförmörkelse
Vi vet att solförmörkelser beror på att månen kommer in mellan solen och jorden, och kastar sin skugga på jorden. Men det har man inte alltid vetat.Tänk dig ett förhistoriskt samhälle. Plötsligt försvinner solen från himlen, och det blir alldeles mörkt! Vad gör man?
Vi vet naturligtvis inte exakt vad de gjorde, men det är inte svårt att tänka sig att människor frågar sig vad de har gjort för att deras gudar/anfäder ska straffa dem så hårt. De höjer sina röster i bön, och efter en stund blidkas tydligen gudarna: Solen tittar fram igen.
Kan man se detta som ett bevis på att deras gudar existerar? Varför/varför inte?
En fjärde lustighet: Mordfrekvens och Internet Explorer
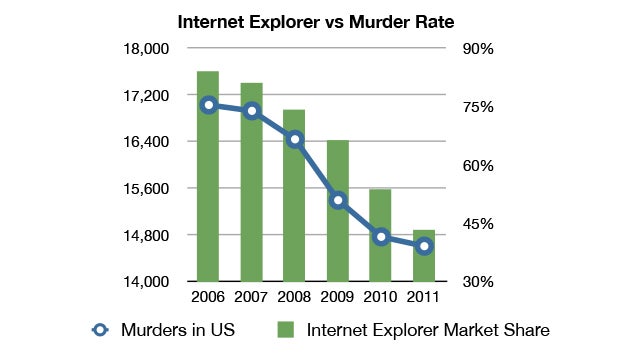Internet Explorer och mordfrekvensen i USA. Är det så att människor blir mindre frustrerade, och mindre benägna att ta till dödligt våld om de använder andra webbläsare än Internet Explorer?
(OBS! Ta siffrorna i diagrammet med en stor nypa salt – jag har inte den blekaste aning om de faktiskt stämmer. Men de ser rätt kul ut ändå!) 
Ännu fler tveksamma korrelationer finns på tylervigen.com.
