Magnus Ehingers undervisning

— Allt du behöver för A i Biologi, Kemi, Bioteknik, Gymnasiearbete med mera.

Artikelindex

Tid: 75 minuter

  • Tillåtna hjälpmedel är penna, suddgummi och linjal, formelsamling, samt miniräknare.
  • Alla svar ska skrivas på ett annat papper. Detta papper kan du behålla om du vill.
  • Alla reaktionsformler skall vara balanserade med minsta möjliga heltalskoefficienter.
  • Antalet poäng per uppgift ges på formen (G/VG/MVG). Exempel: Intill en fråga står det ”(1/1/0)”. Det betyder att man kan få maximalt 1 G-poäng och 1 VG-poäng.

Del I. Endast svar behöver anges. Glöm inte enhet!

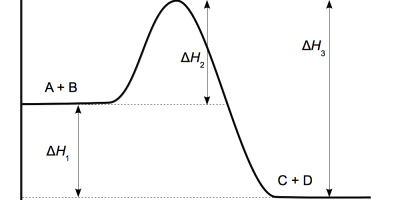
  1. I ett lufttätt kärl har jämvikten

    N2O4(g)

     ⇌

    2NO2(g)

    ∆H > 0 för reaktionen åt höger
    färglös   rödbrun 

    fått ställa in sig. Dikvävetetraoxiden, N2O4, är färglös, medan kvävedioxiden, NO2, är rödbrun.
    1. Ställ upp jämviktsekvationen för reaktionen. (1/0/0)
    2. Vad händer med gasblandningens färg om man tillsätter mer N2O4? (1/0/0)
    3. Vad händer med gasblandningens färg om man ökar trycket i kärlet? (0/1/0)
    4. Vad händer med gasblandningens färg om man minskar temperaturen på reaktionsblandningen? (0/1/0)
  2. Vilket pH har en lösning
    1. som består av 0,250 mol/dm3 salpetersyra, HNO3? (1/0/0)
    2. där [OH–] = 0,025 mol/dm3? (0/1/0)
  3. Vid 45 °C är vattnets jonprodukt Kw = 4,0·10-14 M2. Vilket pH har rent vatten vid 45 °C? (0/1/0)
    1. 2,0
    2. 6,7
    3. 7,0
    4. 7,3
    5. 13,4
    6. 14,0

Del II. Fullständiga lösningar ska redovisas. Glöm inte enhet!

  1. Vid 700 °C mätte man halten SO3, NO, SO2 och NO2 i ett lufttätt reaktionskärl där följande jämvikt ställt in sig:

    SO2(g) + NO2(g) ⇌ SO3(g) + NO(g)

    De värden man fick var: [SO2] = 0,12 M; [NO2] = 0,18 M; [SO3] = 0,32 M; [NO] = 0,11 M. Vilket värde hade jämviktskonstanten K? (1/0/0)
  2. Man löser lite dinatriumvätefosfat, Na2HPO4 i vatten. Vilken reaktion får lösningen: Sur, neutral eller basisk? Motivera ditt svar. (1/1/0)
  3. Vid 25 °C är jämviktskonstanten K = 0,46 för nedanstående reaktion:

    2BrCl ⇌ Br2 + Cl2

    Vid ett visst tillfälle är [BrCl] = 0,30 M; [Br2] = 0,15 M och [Cl2] = 0,15 M.
    1. Visa att systemet inte är i jämvikt (1/0/0)
    2. Åt vilket håll kommer reaktionen att gå? Motivera ditt svar! (1/1/0)
  4. Du tillverkar en buffert genom att blanda 25,0 ml 0,100 M NH3 med 75,0 ml 0,250 M NH4Cl. Beräkna buffertens pH. (1/1/0)
  5. Du har 0,250 dm3 av en lösning med 1,50 M ättiksyra. Vilket är lösningens pH? (2/2/0)
  6. Polyakrylamid, [-CH2-CH(C(O)NH2)-]n, är en polymer av akrylamid, CH2CHC(O)NH2. Det betyder att polyakrylamid är ett stort ämne som är uppbyggt av många små akrylamid-rester. Polyakrylamid är helt ofarligt, medan akrylamid är giftigt och kan skada nervsystemet allvarligt.

    När man tillverkar polyakrylamid kan det göras enligt följande kemiska reaktionsformel:

    n    CH2CHC(O)NH2 ⇌ [-CH2-CH(C(O)NH2)-]n

    Eller, med strukturformler:

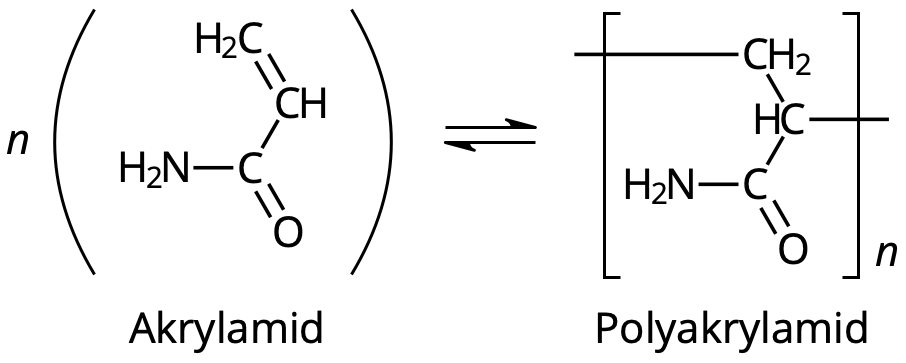
    Syntes av polyakrylamid.

    Reaktionen är en jämvikt som är starkt förskjuten åt höger.

    Det kan vara en riktigt dum idé att försöka täta väggarna i tunneln genom Hallandsåsen med polyakrylamid. Använd både kemiska argument, beräkningar och ekologiska argument för att förklara varför! (2/2/2)

Facit

Betygsgränser

Max: 25 12/11/2
Medel: 14,2 8,9/5,1/0,19
G: 8,0  
VG: 14,5 varav minst 5,5 VGp eller MVGp
MVG: 20,0 varav minst 8,5 VGp och 1 MVGp

Del I. Endast svar krävs.

Ingen/felaktig enhet i svaret … -1p

Räknat med avrundade siffror … -0,5p

    1. \(K = \frac {[\text{NO}_2]^2}{[\text{N}_2\text{O}_4]}\)
    2. Den blir mer rödbrun
    3. Den blir mindre rödbrun
    4. Den blir mindre rödbrun
    1. pH = 0,60
    2. pH = 12,40
  3. b)

    Lösning: I rent vatten (neutralt) är [H+] = [OH–]. Eftersom

    Kw = [H+][OH–]

    får vi att

    \([\text{H}^+] = \sqrt{4,0 \cdot 10^{-14}\text{M}^2} = 0,00000020\text{M}\)

    och

    \(\text{pH} = -\lg{[\text{H}^+]} = -\lg0,00000020 = 6,698970004 \approx 6,70\)

Del II. Frågor som kräver fullständig lösning och (i förekommande fall) balanserade formler. Glöm inte enhet!

  1. \(K = \frac {[\text{SO}_3\text{(g)}][\text{NO}\text{(g)}]}{[\text{SO}_2\text{(g)}][\text{NO}_2\text{(g)}]} = 1,62962963 \approx 1,6\)

  2. \(K_{\text{a, HPO}_4^{2-}} = 4,4 \cdot 10^{-13}\text{M}\)

    \(K_{\text{b, HPO}_4^{2-}} = 1,6 \cdot 10^{-7}\text{M}\)

    \(K_{\text{a, HPO}_4^{2-}} < K_{\text{b, HPO}_4^{2-}}\) … (1/0/0)

    Eftersom \({\sf \text{HPO}_4^{2-}}\) är en mycket svag syra (och måttligt stark bas) blir lösningen basisk. … (0/1/0)

    1. \(Q = \frac {[\text{Br}_2][\text{Cl}_2]}{[\text{BrCl}]^2} = \frac {0,15\text{M} \cdot 0,15\text{M}}{0,30\text{M}^2} = 0,25\)

      Eftersom \(Q \neq K\) är systemet inte i jämvikt.

    2. Om \(Q\) ska närma sig \(K\), måste \(Q\) bli större. Det kan det bara bli om [Br2] och [Cl2] ökar, samtidigt som [BrCl] minskar. Därför kommer reaktionen att gå åt höger.

  4. Buffertformeln ger att

    \(\text{pH} = \text{p}K_{\text{a}} - \log \left(\frac {c_{\text{syra}}}{c_{\text{bas}}} \right )\)

    \(c_{\text{syra}} = \frac {75\text{ml} \cdot 0,250\text{M}}{(25+75)\text{ml}} = 0,1875\text{M}\)

    \(c_{\text{bas}} = \frac {25\text{ml} \cdot 0,100\text{M}}{(25+75)\text{ml}} = 0,0250\text{M}\)

    \(\text{p}K_{\text{a, NH}_4^+} = 9,25\) (från tabell) … (0/1/0)

    \(\text{pH} = 9,25 - \log \left(\frac {0,1875}{0,0250} \right ) = 8,37493874 \approx 8,37\)… (1/0/0)

  5. HAc ⇌ H+ + Ac–

     

    HAc

    H+

    Ac–

    f.r.

    1,50 M

    0

    0

    Δ

    -x

    +x

    +x

    v.j.

    (1,50 - x)M

    xM

    xM

    \(K_{\text{a}} = \frac {[\text{H}^+][\text{Ac}^-]}{[\text{HAc}]}\) … (1/0/0)

    \(K_{\text{a}} = 10^{-4,75}\text{M}\) (från tabell)

    \(10^{-4,75} = \frac {x^2}{1,50 - x} \approx \frac {x^2}{1,50}\)

    \(10^{-4,75} \cdot 1,50 = x^2\)

    \(x = \sqrt{10^{-4,75} \cdot 1,50} = 0,0051647063 = [\text{H}^+]\) … (0/1/0)

    Eftersom x << 1,50 går det bra att försumma x bredvid 1,50. … (0/1/0)

    pH = –log[H+] = –log0,0051647063 = 2,28695437 ≈ 2,29 … (1/0/0)

  6. Eleven tar upp antingen kemiska argument, beräkningar eller ekologiska argument, och diskuterar dessa översiktligt. (1-2/0/0)

    Eleven tar upp åtminstone två av kemiska argument, beräkningar och ekologiska ar-gument, och diskuterar dessa utförligt (1-2/1-2/0)

    Eleven tar upp både kemiska argument, beräkningar och ekologiska argument, och diskuterar dessa utförligt och nyanserat. (1-2/1-2/1-2)