Plocka fram
- I2(s)
- Bägare
- Rundkolv, som passar i bägaren
- Värmeplatta
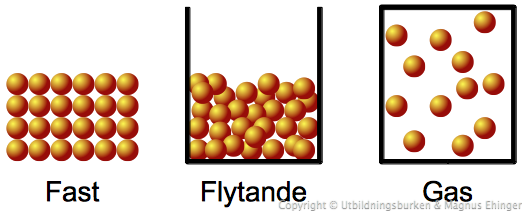
Vad är en gas?
Jämför fast-flytande-gas i olika slutna kärl (rita på tavlan).
Gör sublimeringsexperiment med I2(s).
- Diskutera med eleverna vad som händer!
Gaser fyller hela behållaren.
Gaser kan pressas samman.
Gaser utövar tryck mot kärlets samtliga väggar.
Kinetisk gasteori hjälper att förklara gasernas egenskaper.
- Det är detta vi ska ägna oss åt en stund nu!
Tryck, temperatur och volym
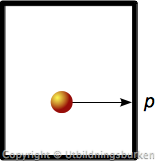
Vad är tryck?
Gasmolekyler är ständigt i rörelse.
- Väldigt fort.
- Syrgas, O2 , i luft: 480 m/s
- Väldigt kort (innan de krockar och ändrar riktning).
- Syrgas i luft: 0,1 μm = en tiomiljondels meter
Var gång en gasmolekyl slår emot "väggen": Den utövar ett tryck!
Förhållandet mellan mängden gas (\(n\)) och trycket (\(p\))
Fråga eleverna, vad händer om vi bara har en enda gasmolekyl i en burk: Högt eller lågt tryck?
- Lågt, eftersom gasmolekylen endast sällan slår i väggen, och med ganska liten kraft.
Fråga eleverna, vad händer om vi har två - fyra - åtta - en mol gasmolekyler i en burk: Högre eller lägre tryck?
Alltså, ju fler molekyler, desto högre tryck. Detta kan man uttrycka lite komplicerat:
- Trycket är proportionellt mot substansmängden (vid konstant volym och temperatur).
eller
- \(p=k_1 \cdot n\) (\(T\), \(V\) konstanta)
Partialtryck
Summan av partialtrycken (varje enskild gas' tryck) = totaltrycket.
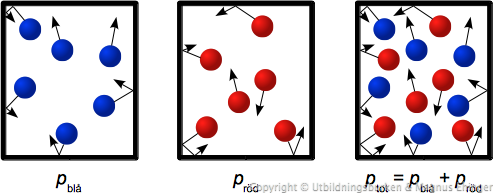
Tänk dig en sluten burk, "fylld" med blåa gasmolekyler.
- Hur är trycket här? Låt oss säga, "högt". Eller varför inte, \(p_{\text{blå}}\).
Tänk dig en sluten burk till, "fylld" den med röda gasmolekyler.
- Hur är trycket här? Låt oss säga, "högt" även här – eller \(p_{\text{röd}}\).
Om vi nu slår samman de båda burkarna till en enda burk, med samma volym - hur blir trycket här?
- Dubbelt så högt!
Detta medför att:
- \(p_{\text{blå}} + p_{\text{röd}} = p_{\text{tot}}\)
Vill man drämma till med riktig matematiska kan man skriva:
- \(p_{\text{tot}} = p_1 + p_2 +...+p_n\)
Eller varför inte:
\[p_{\text{tot}} = \sum_{i=1}^{n}p_i\]
😉
Förhållandet mellan temperatur (\(T\)) och tryck (\(p\))
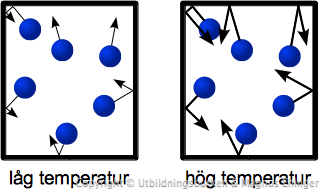
Fråga eleverna, vad innebär temperatur?
- Att molekylerna rör sig.
- Ju högre temperatur, desto mer (fortare) rör sig molekylerna!
Fråga eleverna, om gasmolekylerna rör sig fortare vid högre temperatur, vad innebär det för trycket?
- Jo, när molekylerna "slår i väggen", har de högre hastighet (och större rörelsemängd – här var det dags för lite fysik mitt i alltihopa), och därför blir trycket högre.
Detta medför att ju högre temperatur, desto högre tryck. Detta kan man uttrycka lite mer komplicerat:
- Temperaturen är proportionell mot trycket (vid konstant volym och substansmängd).
eller
- \(p=k_2 \cdot T\) (\(V\), \(n\) konstanta)
Olika gaser vid samma temperatur har samma rörelseenergi.
- Energin: \(W = \frac {mv^2}{2}\)
- Detta ger oss att hastigheten \(v = \sqrt{\frac {2W}{m}}\).
- Vad betyder detta? Jo, ju högre massa partiklarna i en gas har, desto långsammare rör de sig.
Förhållandet mellan volym (\(V\)) och tryck (\(p\))
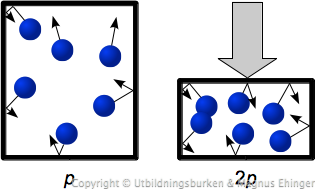
Låt oss säga att vi trycker ihop burken med de blåa gasmolekylerna
Nu blir det fler gasmolekyler per volymsenhet!
Vad innebär detta för trycket?
- Fler gasmolekyler, ja då ökar trycket.
Detta kan vi formulera lite mer komplicerat:
- Trycket är omvänt proportionellt mot volymen (temperatur och substansmängd konstanta).
eller
- \(p = k_3 \cdot \frac {1}{V}\) (\(T\), \(n\) konstanta)
d.v.s.
- \(pV = k_3\) (Boyles lag)
(d.v.s. produkten mellan tryck och volym är konstant för en viss gasmängd vid en viss temperatur).
Räkna exempel 10.1 i boken
Allmänna gaslagen (gasernas allmänna tillståndsekvation)
Alla dessa samband kan vi ställa samman till en enda lag om gaser (allmänna gaslagen):
\[p = (k_1 \cdot n) \cdot (k_2 \cdot T) \cdot \left(k_3 \cdot \frac {1}{V}\right) =\underbrace{k_1 \cdot k_2 \cdot k_3}_{=R} \cdot \frac {nT}{V}\]
alltså
\[p = R \cdot \frac {nT}{V}\]
eller
\[pV=nRT\]
där
- \(p\) är trycket i Pa (N/m2)
- \(V\) är volymen i m3
- \(n\) är substansmängden i mol
- \(T\) är temperaturen i K
- \(R\) är allmänna gaskonstanten, som är 8,314 Nm·mol-1 ·K-1 eller J·mol-1 ·K-1
Gasmolvolym
Hur stor volym har 1 mol av en gas vid STP?
Vi räknar ut det!
\[pV = nRT \Leftrightarrow V = \frac {nRT}{p} \hspace{100cm}\]
\[n = 1\text{mol} \hspace{100cm}\]
\[R = 8,314 \frac {\text{J}}{\text{mol}\cdot \text{K}} \hspace{100cm}\]
\[T = 298\text{K} \hspace{100cm}\]
\[p = 101,3\text{kPa} \hspace{100cm}\]
\[V = \frac {1\text{mol} \cdot 8,314\frac {\text{Nm}}{\text{molK}} \cdot 298\text{K}}{1,013\cdot10^{5}\frac{\text{N}}{\text{m}^2}} \approx 2,45 \cdot 10^{-2}\text{m}^3 = 24,5\text{dm}^3 \hspace{100cm}\]
Praktiskt att veta om man ska blanda gaser: Vid normalt tryck och temperatur är volymen av en mol gas alltid 24,5 dm3! 😊
Vi kan skriva:
\[V = V_{\text{m}} \cdot n \hspace{100cm}\]
\(V\) är volymen i dm3
\(V_{\text{m}}\) är molvolymen i dm3/mol
\(n\) är substansmängden i mol
Ett exempel
Hur stor substansmängd är 6,00 dm3 vätgas vid STP?
Lösning
Vid STP är molvolymen Vm = 24,5 dm3/mol. Vi kan beräkna substansmängden:
\[V = V_{\text{m}} \cdot n \Leftrightarrow n = \frac {V}{V_{\text{m}}} \hspace{100cm}\]
\[n = \frac {6,00\text{dm}^3}{24,5\text{dm}^3/\text{mol}} = 0,24489796\mathrm{mol} \approx 0,245\text{mol} \hspace{100cm}\]