Tid: 75 minuter
Tillåtna hjälpmedel är penna, suddgummi och linjal, formelsamling, utdelat papper med aminosyror samt miniräknare. Samtliga svar ska skrivas på annat papper. Alla reaktionsformler ska vara balanserade med minsta möjliga heltalskoefficienter. I strukturformler ska samtliga atomer sättas ut, även väteatomer. Molvolymen kan antas vara 24,5 dm3/mol och pKw 14,00 om inget annat anges. Andra konstanter etc. får du söka efter i formelsamlingen.
Hoppa direkt till …
Del I. Frågor som bara kräver svar
- 0,0250 m3 av en viss gas har massan 0,125 kg vid 23,0°C och trycket 101,3 kPa. Vilken är gasens
- substansmängd? (1p)
- molmassa? (1p)
- Jämviktskonstanten vid en viss temperatur är 4,8·10-6 för nedanstående reversibla reaktion.
2ICl(g) ⇌ I2(g) + Cl2(g)
Vad blir jämviktskonstanten för den omvända reaktionen, I2(g) + Cl2(g) ⇌ 2ICl(g)? (1p)
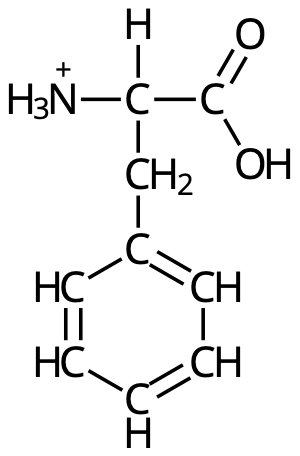
- Aminosyran fenylalanin har Ip = 5,8. Skriv strukturformeln för den form av fenylalanin som dominerar vid pH = 1. (1p)
- Väteperoxid, H2O2, reagerar i sur lösning med permanganatjoner, MnO\({\sf _4^-}\), under bildning av manganjoner, Mn2+, och syrgas. Skriv den balanserade formeln för reaktionen! (2p)
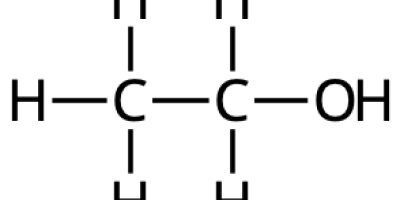
- Om du oxiderar glykol med ett måttligt oxidationsmedel kan ett antal olika produkter bildas innan molekylen bryts sönder till koldioxid och vatten. Ange strukturformel och namn för den mest oxiderade av dessa produkter! Du kan ange rationellt namn eller trivialnamn på produkten. (2p)
- Vilka tre utav följande katabola processer äger rum i mitokondrien eller dess membran? (2p)
- Betaoxidation
- Cellandning
- Citronsyracykeln
- Glykolys
- Transaminering
Del II. Frågor som kräver fullständig lösning och (i förekommande fall) balanserade formler. Glöm inte enhet!
- I en viss galvanisk cell är emk = 1,21 V. Cellreaktionen är
Sn2+(aq) + Cl2(g) → Sn4+(aq) + 2Cl–(aq)
och "klorelektroden" är positiv pol. Skriv cellschemat för den galvaniska cellen, och beräkna \(e^0_{\text{Sn}_4^+/\text{Sn}^{2+}}\). (2p)
- Är det möjligt att göra en gelfiltreringskolonn som kan separera maltos från cellobios i en lösning? Utgå ifrån hur en gelfiltreringskolonn fungerar, och diskutera gelfiltreringens möjligheter. (3p)
- I ett försök blandade man svaveldioxid och kvävedioxid i ett lufttätt kärl. Efter ett tag ställde följande jämvikt in sig:
SO2(g) + NO2(g) ⇌ SO3(g) + NO(g)
Vid jämvikt fann man att man hade fått 0,30 mol SO3, 0,20 mol NO, 0,050 mol NO2 och 0,40 mol SO2. Nu ville man öka substansmängden NO2 till 0,30 mol. Hur stor substansmängd NO måste man då tillföra? Volym och temperatur hölls konstanta. (3p)
- Det vita färgämnet litopon, som bland annat används i vattenbaserad målarfärg, är en blandning mellan zinksulfid och bariumsulfat. Det framställs genom följande reaktion:
BaS(aq) + ZnSO4(aq) → ZnS(s) + BaSO4(s)
Beräkna massan litopon som maximalt kan bildas om man blandar 275 ml 0,350 M bariumsulfidlösning med 325 ml 0,280 M zinksulfatlösning! (3p)
- Man framställde en buffertlösning genom att blanda 10,7 g ammoniumklorid, NH4Cl, med 0,10 mol ammoniak i så mycket vatten att lösningens slutvolym blev 500 cm3. Beräkna lösningens pH! \(\text{p}K_{\text{b, NH}_3} = 4,70\). (4p)
Facit
Betygsgränser
| Max: | 25,0 |
| G: | 7,5 |
| VG: | 15,0 |
| MVG: | 20,0 |
Del I. Frågor som bara kräver ett kort svar
- \[\begin{align}pV &= nRT \Leftrightarrow n = {{pV} \over {nRT}} = \hspace{100cm} \\ &= \frac {101,3 \cdot 10^3\text{Pa} \cdot 0,0250\text{m}^3}{8,314 \frac{\text{J}}{\text{molK}}} = 1,0290766\text{mol} \approx 1,03 \text{mol}\end{align}\]
- \[M = \frac{m}{n} = \frac{125\text{g}}{1,0290766\text{mol}} = 121,46811\text{g/mol} \approx 121\text{g/mol} \hspace{100cm}\]
- \[K_2 = \frac{1}{K_1} = \frac {1}{4,8 \cdot 10^{-6}} = 2,1 \cdot 10^5 \hspace{100cm}\]
- 6H+ + 5H2O2 + 2MnO\({\sf _4^-}\) → 2Mn2+ + 5O2 + 8H2O
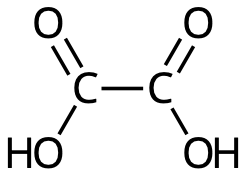
- oxalsyra (1,2-etandisyra),
- a, b, c
Del II. Frågor som kräver fullständig lösning och (i förekommande fall) balanserade formler. Glöm inte enhet!
Ingen/felaktig enhet i svaret ... –1p
Räknat med avrundade siffror ... –0,5p
- – Pt(s) | Sn2+(aq), Sn4+(aq) || Cl–(aq) | Pt(s), Cl2(g) +
\[E = e^0_+ - e^0_- = e^0_{\text{Cl/Cl}^-} - e^0_{\text{Sn}^{4+}/\text{Sn}^{2+}} \hspace{100cm}\]
\[e^0_{\text{Sn}^{4+}/\text{Sn}^{2+}} = e^0_{\text{Cl/Cl}^-} - E = 1,36\text{V} - 1,21\text{V} = 0,15\text{V} \hspace{100cm}\]
Rätt cellschema – 1p; rätt beräkning på normalpotentialen – 1p.
- Redogörelse för hur gelfiltrering fungerar, och vilka ämnen som separerar ut först – 2p; Förklaring varför maltos och cellobios inte kan separeras med gelfiltrering – 1p.
- \[K = \frac {[\text{SO}_3][\text{NO}]}{[\text{SO}_2][\text{NO}_2]} = \frac {0,30 \cdot 0,20}{0,40 \cdot 0,050} = 3 \hspace{100cm}\]
SO2(g)
+
NO2(g)
⇌
SO3(g)
+
NO(g)
Före j.v.
0,40
0,050
0,30
0,20+x
mol
Förändring
+0,25
+0,25
-0,25
-0,25
mol
Vid j.v.
0,65
0,30
0,05
x-0,05
mol
\[K = \frac {[\text{SO}_3][\text{NO}]}{[\text{SO}_2][\text{NO}_2]} \hspace{100cm}\]
\[3 = \frac {0,05 \cdot (x-0,05)}{0,65 \cdot 0,30} = \frac {0,05x-0,0025}{0,195} \hspace{100cm}\]
\[3 \cdot 0,195 = 0,05x - 0,0025 \hspace{100cm}\]
\[x = \frac {3 \cdot 0,195 + 0,0025}{0,05} = 11,75 \hspace{100cm}\]
Man måste tillsätta 11,75 mol NO.
Rätt beräkning av \(K\) – 1p; rätt uppställning för förskjutning av jämviktsläget – 1p; rätt beräkning av tillsatt mängd NO(g) – 1p.
- \[\begin{align}n_{\text{BaS}} &= c_{\text{BaS}} \cdot V_{\text{BaS}} = \hspace{100cm} \\ &= 0,275\text{dm}^3 \cdot 0,350 \text{mol/dm}^3 = 0,09625\text{mol}\end{align}\]
\[\begin{align}n_{\text{ZnSO}_4} &= c_{\text{ZnSO}_4} \cdot V_{\text{ZnSO}_4} = \hspace{100cm} \\ &= 0,325\text{dm}^3 \cdot 0,280\text{mol/dm}^3 = 0,091\text{mol}\end{align}\]
Substansmängden ZnSO4 är begränsande. Eftersom molförhållandena är 1:1 hela vägen, kommer det att bildas 0,091 mol ZnS och 0,091 mol BaSO4.
\[\begin{align}m_{\text{ZnS}} &= n_{\text{ZnS}} \cdot M_{\text{ZnS}} = \hspace{100cm} \\ &= 0,091\text{mol} \cdot (65,4 + 32,1)\text{g/mol} = 8,8725\text{g}\end{align}\]
\[\begin{align}m_{\text{BaSO}_4} &= n_{\text{BaSO}_4} \cdot M_{\text{BaSO}_4} = \hspace{100cm} \\ &= 0,091\text{mol} \cdot (137,3+32,1+16,0\cdot 4)\text{g/mol)} = 21,2394\text{g}\end{align}\]
\[m_{\text{tot}} = m_{\text{ZnS}} + m_{\text{BaSO}_4} = 30,1119\text{g} \approx 30,1\text{g} \hspace{100cm}\]
Rätt substansmängder BaS & ZnSO4 – 1p; rätt massor ZnS & BaSO4 – 1p; rätt mtot – 1p.
- pKa = 14,00 - 4,70 = 9,3 ⇒ Ka = 10-9,3M
\[\begin{align}c_{\text{NH}_4\text{Cl}} &= \frac {n_{\text{NH}_4\text{Cl}}}{V_{\text{NH}_4\text{Cl}}} = \frac {m_{\text{NH}_4\text{Cl}}}{M_{\text{NH}_4\text{Cl}} \cdot V_{\text{NH}_4\text{Cl}}} = \hspace{100cm} \\ &= \frac {10,7\text{g}}{53,532\text{g/mol} \cdot 0,500\text{dm}^3} = 0,3997608\text{mol/dm}^3 \approx 0,4\text{M}\end{align}\]
NH\(_4^+\)
⇌
NH3+
+
H+
Före j.v.
0,40
0,20
0
M
Förändring
-x
+x
+x
M
Vid j.v.
0,40-x
0,20 + x
x
M
\[K_{\text{a}} = \frac {[\text{NH}_3][\text{H}^+]}{[\text{NH}_4^+]} \hspace{100cm}\]
\[10^{-9,3} = \frac {(0,20+x) \cdot x}{0,40-x} \approx \frac {0,20x}{0,40} \hspace{100cm}\]
\[x = \frac {0,40}{0,20} \cdot 10^{-9,3} = 1,00177 \cdot 10^{-9} \hspace{100cm}\]
\[\text{pH} = -\lg(1,00177 \cdot 10^{-9}) = 8,9992297 \approx 9,00 \hspace{100cm}\]
Korrekt uträkning av \(K_\mathrm{a}\) – 1p; korrekt uträkning av ursprungskoncentrationerna – 1p; korrekt uppställning av jämviktsförändringen – 1p; korrekt beräkning av pH – 1p.