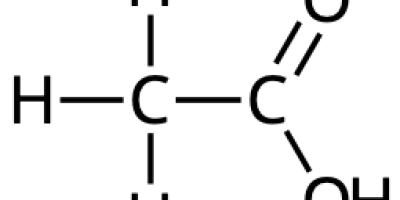Tid: 90 minuter
Tillåtna hjälpmedel: Formelsamling, miniräknare.
Buffertformeln:
\[[\text{H}^+] = K_\text{a} \cdot \frac {c_\text{syra}}{c_\text{bas}}; \text{ pH}=\text{p}K_\text{a}-\lg\left(\frac {c_\text{syra}}{c_\text{bas}} \right)\]
Betygsmatris
Dina svar kommer att bedömas enligt nedanstående matris:
|
| E | C | A |
| Begrepp, modeller, teorier och arbetsmetoder | Eleven redogör översiktligt för innebörden av dem | … utförligt … | … utförligt och nyanserat … |
| Svara på frågor om och beskriva kemiska företeelser och förlopp | Med viss säkerhet, exemplifierar | Med viss säkerhet, exemplifierar | Med säkerhet, exemplifierar och generaliserar kring |
| Analysera och besvara frågor | Enkla frågor i bekanta situationer med tillfredsställande resultat | Komplexa … bekanta situationer … tillfredsställande … | Komplexa … bekanta och nya situationer … gott … |
| Språk och kommunikation | Eleven använder med viss säkerhet ett naturvetenskapligt språk och anpassar till viss del sin kommunikation till syfte och sammanhang. | … med viss säkerhet … till stor del … | … med säkerhet … till stor del … |
Vid varje fråga står det vad som bedöms och på vilken nivå du kan besvara frågan.
Språklig bedömning
På hela provet gör jag också en samlad bedömning av hur du använder det vetenskapliga språket (se betygsmatrisen ovan). På det här provet handlar det framför allt om hur du ställer upp dina beräkningar, att de är lätta att följa, att du använder storhet, mätetal och enhet på ett korrekt sätt och så vidare.
Språk och kommunikation (1/1/1)
Hoppa direkt till …
Del I. Endast ett kort svar (ett ord eller 1-2 meningar) behövs
- Skriv reaktionsformeln för den reaktion som sker när salpetersyra, HNO3, neutraliseras av natriumhydroxid, NaOH.
Svara på frågor om och beskriva kemiska företeelser och förlopp (1/0/0)
- Vilken är den korresponderande syran till ammoniak, NH3?
Svara på frågor om och beskriva kemiska företeelser och förlopp (1/0/0)
- Vätecyanid, HCN, är en svag syra. Teckna uttrycket för syrakonstanten för vätecyanid.
Begrepp, modeller, teorier och arbetsmetoder (1/0/0)
- Vilka partiklar (förutom vatten) finns i en lösning av ättiksyra, HAc(aq)?
Svara på frågor om och beskriva kemiska företeelser och förlopp (1/1/0)
Del II. Ringa in de rätta alternativen!
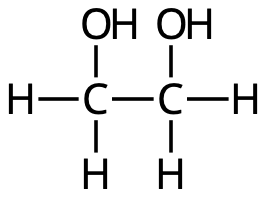
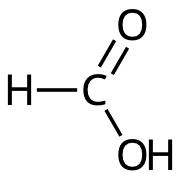
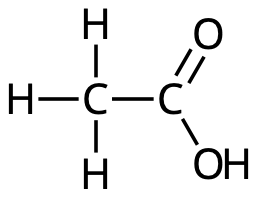
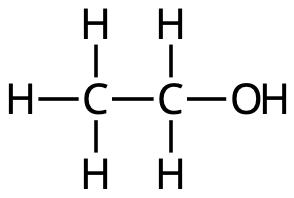
- Vilken av nedanstående bilder visar strukturformeln för ättiksyra?
- Vilken reaktion får en lösning av dinatriumvätefosfat, Na2HPO4(aq)?
- Starkt sur
- Svagt sur
- Neutral
- Svagt basisk
- Starkt basisk
- Formeln för divätefosfatjonens, H2PO\(_4^-\), protolys kan skrivas
| H2PO\(_4^-\) | + | H2O | ⇌ | HPO\(_4^{2-}\) | + | H3O+ |
| α | β | γ | δ |
Vilka två av följande påståenden är korrekta?
- α och δ är ett syra–bas-par
- α och β är ett syra–bas-par
- β och γ fungerar som baser i den här reaktionen.
- β är korresponderande bas till δ i den här reaktionen.
- α är korresponderande bas till γ i den här reaktionen.
Del III. Frågor som kräver ett utredande svar (fullständiga beräkningar krävs)
Skriv svaren på de här frågorna på ett annat papper.
- I så kallad PBS (fosfatbuffrad saltlösning) utnyttjas den buffrande förmågan hos följande jämviktssystem:
H2PO\(_4^-\) + H2O ⇌ HPO\(_4^{2-}\) + H3O+
Förklara med hjälp av reaktionsformler och Le Chateliers princip varför pH inte förändras nämnvärt i en PBS-lösning om man tillsätter en måttlig mängd syra (H3O+) eller bas (OH–). - På ditt kemilaboratorium vill du en dag framställa 0,500 dm3 buffert med pH = 9,00. Du bestämmer dig för att lösa lite fast ammoniumklorid, NH4Cl(s), till en total volym på 0,500 dm3 0,20 M ammoniaklösning. Hur stor massa ammoniumklorid behövs för att buffertens pH ska bli 9,00? För ammoniumjonen gäller att \(K_{\text{a, NH}_4^+} = 5,6\cdot 10^{-10}\text{M}\).
- Barbitursyra, HC4H3N2O3, är en svag syra vars pKa = 4,0. Barbitursyran används för att framställa så kallade barbiturater, en grupp av lugnande läkemedel. Beräkna pH i en lösning där man löst 15 g barbitursyra i vatten till en total volym på 0,250 dm3.
Facit
Betygsgränser
| Max: | 20,0 | (10/6/4) | |
| Medel: | |||
| E: | 7,5 | ||
| D: | 10,5 | varav | 3,0 A- eller C-poäng |
| C: | 13,5 | varav | 4,5 A- eller C-poäng |
| B: | 15,5 | varav | 2,0 A-poäng |
| A: | 17,5 | varav | 3,0 A-poäng |
Del I. Endast ett kort svar (ett ord eller 1-2 meningar) behövs
- HNO3 + NaOH → NaNO3 + H2O
- NH\(_4^+\) (ammoniumjon)
- \(K_\text{a}=\frac {[\text{H}^+][\text{CN}^-]}{[\text{HCN}]}\) eller \(K_\text{a}=\frac {[\text{H}_3\text{O}^+][\text{CN}^-]}{[\text{HCN}]}\)
- HAc, Ac–, H3O+, OH–
E – Eleven anger korrekt tre av partiklarna ovan
C – Eleven anger korrekt alla fyra partiklar.
Del II. Ringa in de rätta alternativen!
- e
- d
Motivering:
\(K_{\text{b, HPO}_4^{2-}} = 1,6 \cdot 10^{-7}\text{M}\)
\(K_{\text{a, HPO}_4^{2-}} = 4,4 \cdot 10^{-13}\text{M}\)
Eftersom \(K_{\text{b, HPO}_4^{2-}} > K_{\text{a, HPO}_4^{2-}}\) är vätefosfatjonen starkare som bas än som syra. Därför blir lösningen basisk. Eftersom \(K_{\text{b, HPO}_4^{2-}}\) är relativt litet blir lösningen bara svagt basisk.
Genom att ge svaret (e) har eleven visat att hen behärskar joners protolys på E-nivå. Genom att ge svaret (d) kan eleven även ta hänsyn till att vätefosfatjonen kan fungera både som syra och som bas, och behärskar joners protolys på C-nivå. - c, d
Del III. Frågor som kräver ett utredande svar (fullständiga beräkningar krävs)
- Le Chateliers princip säger att om ett jämviktssystem rubbas, så sker det en nettoreaktion som motverkar rubbningen. Om vi tillsätter mera syra (H3O+) innebär detta att reaktionen kommer att gå åt vänster tills jämviktsläget åter uppnås, och [H3O+] är ungefär densamma som förut:
H2PO\(_4^-\) + H2O ← HPO\(_4^{2-}\) + H3O+
Om man istället tillsätter en bas (OH–) kommer följande reaktion att ske:
H3O+ + OH– → 2H2O
Det betyder att [H3O+] kommer att sjunka. Återigen gäller Le Chateliers princip, och reaktionen kommer att gå åt höger tills jämvikt åter uppnåtts, och [H3O+] återställts:
H2PO\(_4^-\) + H2O → HPO\(_4^{2-}\) + H3O+
Bedömning
E – Eleven gör en ansats till att besvara frågan, till exempel genom att definiera Le Chateliers princip eller förklara hur Le Chateliers princip fungerar.
C – Eleven förklarar utförligt vad som händer när syra eller bas sätts till bufferten.
A – Eleven förklarar utförligt och nyanserat vad som när syra och när bas sätts till bufferten.
Kommentar: I båda förklaringarna måste framgå hur [H3O+] påverkas av tillsatsen syra eller bas.
Språklig bedömning
E – Eleven stöttar sin förklaring med någon korrekt skriven, relevant reaktionsformel.
C – Eleven stöttar sin förklaring med två korrekt skrivna, relevanta reaktionsformler.
A – Eleven stöttar sin förklaring med åtminstone tre korrekt skrivna, relevanta reaktionsformler. - Buffertformeln ger att
\([\text{H}^+] = K_\text{a} \cdot \frac {c_\text{syra}}{c_\text{bas}}\)
\(c_\text{syra} = \frac {[\text{H}^+] \cdot c_\text{bas}}{K_\text{a}} = \frac {10^{-9,00}\cdot 0,20}{5,6 \cdot 10^{-10}}\text{M} = 0,3571428571\text{M}\)
\(n_\text{syra} = c_\text{syra} \cdot V = 0,3571428571\text{mol/dm}^3 \cdot 0,500\text{dm}^3 = 0,1785714286\text{mol}\)
\(m_{\text{NH}_4\text{Cl}} = n_{\text{NH}_4\text{Cl}} \cdot M_{\text{NH}_4\text{Cl}} = 0,1785714286\text{mol} \cdot 53,49\text{g/mol} = 9,5517857\text{g} \approx 9,6\text{g}\)
Bedömning
E – Eleven gör en ansats till att lösa uppgiften, till exempel genom att beräkna någon koncentration eller ställa upp uttrycket för \(c_\text{syra}\).
C – Eleven beräknar \(c_\text{syra}\) korrekt.
A – Eleven beräknar \(m_{\text{NH}_4\text{Cl}}\) korrekt. - Vi kallar barbitursyran HA. Följande protolys sker:
HA ⇌ H+ + A–
\(c_\text{HA} = \frac {n_\text{HA}}{V} = \frac {\frac {m_\text{HA}}{M_\text{HA}}}{V} = \frac {\frac {15\text{g}}{128,09\text{g/mol}}}{250\text{dm}^3} = 0,46842064\text{mol/dm}^3\)
HA H+ A– f. r. \(0,46\text{…}\) \(0\) \(0\) \(\text{M}\) Δ \(–x\) \(+x\) \(+x\) \(\text{M}\) v. j. \((0,46 – x)\) \(x\) \(x\) \(\text{M}\)
\(K_{\text{a}} = \frac {[\text{H}^+][\text{A}^-]}{[\text{HA}]}\)
\(10^{-4,0} = \frac {x \cdot x}{0,46842064-x} \approx \frac {x^2}{0,46842064}\)
\(x = \sqrt{10^{-4,0} \cdot 0,46842064} = 0,00684413\)
Eftersom x << 0,46… går det bra att försumma x bredvid 0,46.
\([\text{H}^+] = x = 0,00684413\text{M}\)
\(\text{pH} = -\lg(0,00684413) = 2,16468199 \approx 2,16\)
Svar mellan 2,1–2,2 är godkända.
Bedömning
Även om det är möjligt att besvara frågan hela vägen från E- till A-nivå väljer jag att bara ge ett A-belägg på den här frågan – för de elever som verkligen vill visa att de når A-nivå.
Om eleven ej visat att \(x\) kan försummas bredvid 0,46, och inte heller löst andragradsekvationen fullständigt, erhålls max 0,5A.