Plocka fram
- Mätcylinder, 100ml
- Mätcylinder, 50 ml
- 2 glasrör
- BTB
Demonstration
Använd de cylindrar vi tidigare uppnått jämvikt med!
Vad händer om vi fyller på ytterligare vatten i den ena cylindern?
Vilket håll går reaktionen åt?
Varför?
Hur blir jämviktskonstanten, då jämvikt åter uppnåtts?
Hur förskjuts jämvikten då koncentrationen ändras?
Betrakta följande reaktion:
H2(g) + I2(g) ⇌ 2HI(g)
Låt oss säga att temperaturen är 425°C. Då är K = 54.
Vi startar med 0,100 mol av både H2 och I2 i ett kärl med volymen 1,00 dm3.
Vilken är koncentrationerna [H2], [I2] och [HI] vid jämvikt?
Lösning
Vi börjar med att teckna jämviktskonstanten för reaktionen:
\[K = \frac {[\text{HI}]^2}{[\text{H}_2][\text{I}_2]} \hspace{100cm}\]
Dags för en tabell! Eftersom vi inte vet hur mycket HI som bildas, kallar vi det för \(x\). Ur reaktionsformeln läser vi att samtidigt som det bildas \(x\) mol HI, så går det åt \(\frac {x}{2}\) mol av varderas H2 och I2.
| [H2] | [I2] | [HI] | ||
| cstart | \[0,100\] | \[0,100\] | \[0\] | M |
| ändring | \[-\frac {x}{2}\] | \[-\frac {x}{2}\] | \[+x\] | M |
| cjämvikt | \[0,100 - \frac {x}{2}\] | \[0,100 - \frac {x}{2}\] | \[x\] | M |
Vi sätter in jämviktskonstanten och värdena i jämviktsekvationen:
\[54 = \frac {x^2}{\left(0,100 - \frac {x}{2} \right )\cdot \left(0,100 - \frac {x}{2} \right )} = \frac {x^2}{\left(0,100 - \frac {x}{2} \right )^2} \hspace{100cm}\]
Vi drar roten ur bägge leden:
\[\sqrt {54} = \sqrt {\frac {x^2}{\left(0,100 - \frac {x}{2} \right )^2} } = \frac {x}{\left(0,100 - \frac {x}{2} \right )}\hspace{100cm}\]
(Vi bortser från den negativa roten, som är orimlig.)
Vi löser ut \(x\):
\[\sqrt {54} \left(0,100 - \frac {x}{2} \right ) = x \hspace{100cm}\]
\[0,100 \cdot \sqrt {54} - \frac {x}{2} \cdot \sqrt {54} = x \hspace{100cm}\]
\[0,100 \cdot \sqrt {54} = x + \frac {x}{2} \cdot \sqrt {54} \hspace{100cm}\]
\[0,100 \cdot \sqrt {54} = \left(1 + \frac {1}{2} \cdot \sqrt {54}\right )x \hspace{100cm}\]
\[\frac {0,100 \cdot \sqrt {54}}{\left(1 + \frac {1}{2} \cdot \sqrt {54}\right )} = x = 0,15721225 \hspace{100cm}\]
Nu kan vi räkna ut koncentrationerna [H2], [I2] och [HI] vid jämvikt:
\[[\text{H}_2] = [\text{I}_2] = \left (0,100 - \frac {0,15721225}{2} \right )\text{M} = 0,02139388\text{M} \approx 0,021\text{M} \hspace{100cm}\]
[HI] = x = 0,15721225M ≈ 0,157M
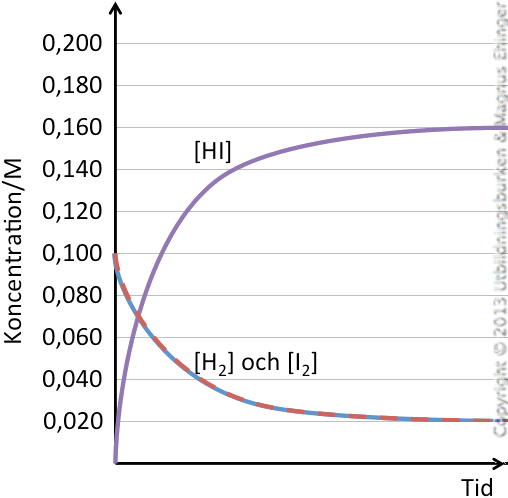
Efter en stund uppnås alltså jämviktskoncentrationerna:
[H2] = 0,021 M
[I2] = 0,021 M
[HI] = 0,158 M
Jämvikten mellan väte, jod och vätejodid ställer in sig.
Hur stor andel (%) av joden har övergått till vätejodid?
- 79%
Nu rubbar vi jämvikten!
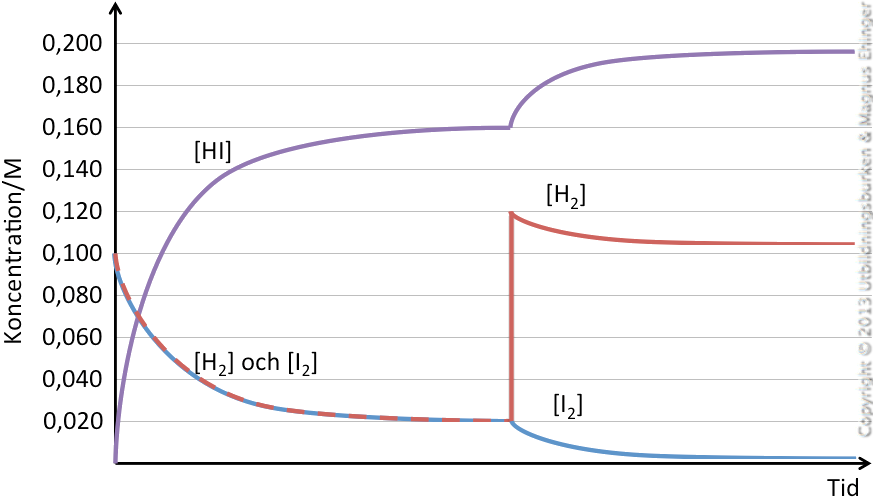
Vi för in ytterligare 0,10 mol väte i jämviktsblandningen. Vad händer?
Vi börjar med att beräkna \(Q\)!
\[Q = \frac {[\text{HI}]^2}{[\text{H}_2][\text{I}_2]} = \frac {(0,157\text{M})^2}{0,121\text{M} \cdot 0,021\text{M}} \approx 9,8 < K = 54 \hspace{100cm}\]
- Vi ser att Q < K, vilket innebär att reaktionen måste gå åt höger: Det bildas mer produkter, allteftersom mängden reaktanter avtar.
Sålunda: Mera väte och jod reagerar och bildar vätejodid!
Jämvikten mellan väte, jod och vätejodid rubbas, och en ny jämvikt ställer in sig.
Jämviktskoncentrationerna beräknas på samma sätt som ovan. De blir till slut:
[H2] = 0,106 M
[I2] = 0,00061 M
[HI] = 0,188 M
Hur stor del av den ursprungliga joden har nu överförts till vätejodid?
- 94%
Le Chateliers princip
Om man gör en förändring i ett jämviktssystem, sker en nettoreaktion på så vis, att förändringen motverkas.
Med andra ord:
Det som sätts in i ena änden, rinner ut i den andra.
😉
