Buffertar fungerar som stötdämpare
Vad är en buffert?
- "Stötdämpare" för förändringar i H+-koncentrationen.
Hur gör man en buffert?
- Blandar en svag syra + dess motsvarande (svaga) bas, i relativt höga koncentrationer.
Exempel
- HAc – Ac–
- NH\(_4^+\) – NH3
- H2CO3 – HCO\(_3^-\) (viktig i våra kroppar!)
Hur en buffert funkar (enligt Le Chateliers princip)
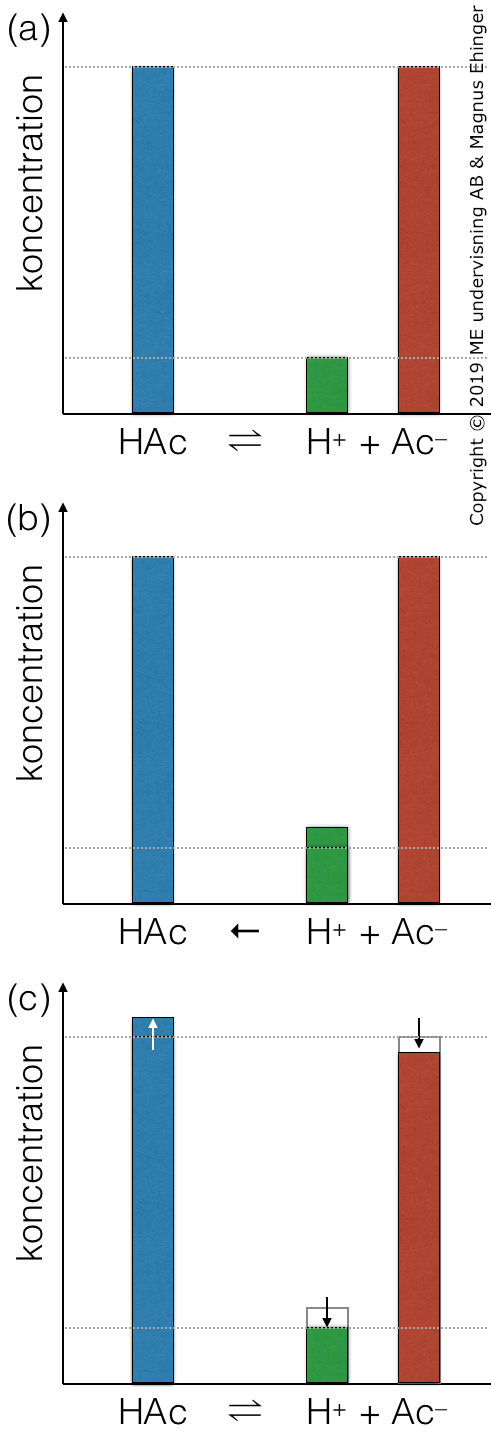
(a) Buffertsystemet är i jämvikt. (b) En liten mängd syra (H+) sätts till lösningen. Jämvikten rubbas, och går åt vänster (enligt Le Chateliers princip). (c) När systemet åter nått jämvikt är koncentrationen H+ åter ungefär lika låg som innan.
(a) Buffertsystemet är i jämvikt. (b) En liten mängd bas (OH–) sätts till lösningen. Den reagerar med H+ och bildar vatten, vilket gör att [H+] sjunker. Jämvikten rubbas, och går åt höger (enligt Le Chateliers princip). (c) När systemet åter nått jämvikt är koncentrationen H+ åter ungefär lika hög som innan.
Beräkning av pH i en buffertlösning
0,10 mol HAc och 0,10 mol NaAc löses i vatten, och spädes till 1,00 l. \(K_\text{a}\) för reaktionen
HAc + H2O ⇌ H3O+ + Ac–
är 1,8 · 10–5 M. Vilket är den spädda lösningens pH?
Lösning
Tabelldags!
|
| [HAc] (M) | [H+] (M) | [Ac–] (M) |
| Före protolys | \[0,10\] | \[0\] | \[0,10\] |
| Ändring | \[-x\] | \[+x\] | \[+x\] |
| Vid jämvikt | \[0,10-x\] | \[x\] | \[0,10+x\] |
Vi beräknar vätejonkoncentrationen \(x\).
\[K_{\text{a}} = \frac {[\text{H}^+][\text{Ac}^-]}{[\text{HAc}]} \Leftrightarrow [\text{H}^+] = K_{\text{a}} \cdot \frac {[\text{HAc}]}{[\text{Ac}^-]} \hspace{100cm}\]
\[x = 1,8\cdot 10^{-5}\text{M} \cdot \frac {(0,10-x)\text{M}}{(0,10+x)\text{M}} \hspace{100cm}\]
Ekvationen går att lösa, men det blir en andragradsekvation. För att förenkla beräkningen, kan vi pröva om det går bra att försumma x bredvid 0,10. (Detta kan vi endast göra om x << 0,10!)
\[x \approx 1,8\cdot 10^{-5}\text{M} \cdot \frac {0,10\text{M}}{0,10\text{M}} \hspace{100cm}\]
\[[\text{H}^+] = x \approx 1,8\cdot 10^{-5}\text{M} \hspace{100cm}\]
Eftersom \(x \ll 0,10\) kan vi konstatera att det går bra att försumma \(x\) bredvid 0,10. Vi beräknar pH:
\[\text{pH} = -\lg(1,8\cdot 10^{-5}) = 4,74 \hspace{100cm}\]
Buffertformeln
\[[\text{H}^+] = K_{\text{a}} \cdot \frac {c_{\text{syra}}}{c_{\text{bas}}} \hspace{100cm}\]
\[\text{pH} = \text{p}K_{\text{a}}-\lg \left(\frac{c_{\text{syra}}}{c_{\text{bas}}}\right) \hspace{100cm}\]
Ett till exempel!
Beräkna pH för lösningen som man får genom att blanda 20,0 ml 0,100 M HAc med 30 ml 0,100 M NaAc!
\[c_{\text{HAc}} = \frac {0,020\text{dm}^3 \cdot 0,100\text{mol/dm}^3}{0,050\text{dm}^3} = 0,0400\text{mol/dm}^3 \hspace{100cm}\]
\[c_{\text{NaAc}} = \frac {0,030\text{dm}^3 \cdot 0,100\text{mol/dm}^3}{0,050\text{dm}^3} = 0,0600\text{mol/dm}^3 \hspace{100cm}\]
Efter jämvikt: [HAc] ≈ 0,0400 M; [Ac–] ≈ 0,0600 M (eftersom ättiksyran HAc protolyseras i så liten omfattning).
\[[\text{H}^+] = 1,8 \cdot 10^{-5}\text{M} \cdot \frac {0,0400\text{M}}{0,0600\text{M}} = 1,2 \cdot 10^{-5}\text{M} \hspace{100cm}\]
\[\text{pH} = -\lg(1,2 \cdot 10^{-5}) = 4,92 \hspace{100cm}\]
